Hallo vrienden, Leo hier. The topic today is the legendary graph A* Algorithm in Swift also called A Start algorithm.
We’ll talk about a very great graph search algorithm called A* ( A Star). This algorithm’s main objective is to find the path in the graph based on some conditions that you can choose, also known as the Heuristic.
We will not run into the deep dive of the A Star algorithm time complexity because depends on the implementation, but we can sure say that one of the greatest drawbacks of the A Star is the space complexity. The A Star depends on saving all the previous paths to compare each one heuristics to decide what’s the next best step toward a target.
Interested in solving the Eight Puzzle with a neat algorithm? Stay with me in this interesting post.
Let’s code! But first…
The Painting of The Day
Today’s painting is Constellation: The Morning Star, a 1940 piece of art from Joan Miro. Since the post it’s about A Star, I found the morning star very suitable to introduce this painter’s work in this blog.
Joan Miró I Ferrà, born on 20 April 1893 and died on 25 December 1983, was a Spanish painter, sculptor, and ceramicist born in Barcelona.
Earning international acclaim, his work has been interpreted as Surrealism, a sandbox for the subconscious mind, a re-creation of the childlike, and a manifestation of Catalan pride. In numerous interviews dating from the 1930s onwards, Miró expressed contempt for conventional painting methods as a way of supporting bourgeois society and famously declared an assassination of painting in favor of upsetting the visual elements of established painting.
The problem
You have an Eight Puzzle to solve.
We all have been in this place before, went to a party or a city fair, and won some little puzzle that has one piece missing and all the other pieces form an image. Like this image below:

Or this:

Now imagine that all the tiles of the puzzle above are numbers like:
let endState = [["1","2","3"],
["4","5","6"],
["7","8","0"]]Where zero means the empty tile. Suddenly we can use a graph search algorithm to solve our problems!
The algorithm – A* Algorithm in Swift
The idea of the algorithm is not very simple but it’s easier when you use images to know what is going on. Imagine the first state would be this:
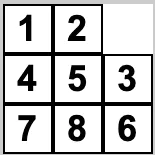
1 Step – of the algorithm is to generate all the possible next moves for this position aggregating with the previous step, in this case, there are two possible board states.
This position:
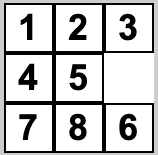
And this position:
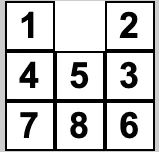
Now the algorithm has two paths. The first position and the second position to choose. Like the image above…
But how does it decide where to go?
For the Second Step, we’ll be using heuristic of course!
“Heuristic” is a 10-dollar word for a 5 cents meaning. The heuristic is just some arbitrary decision that an algorithm has to make to improve its speed/space/etc.
The heuristic chosen was: How many tiles are placed correctly? This way the algorithm will always prioritize the path with fewer misplaced tiles. If you want to optimize space, you could do the algorithm choose the first one, and discard all the others. If you want to prioritize the best solution, you should always keep track of all possibilities and it’s where the A* weakness lives.
The third step is just a check if the algorithm selected the actual solution for the problem and it’s done! If not, go back to step one and try new board configurations until finding the right one.
This would be the final state.
Now let’s explore the algorithm to do that.
The Algorithm – Coding
The code above you can import directly to your Xcode Playground and run it to test.
import Foundation
enum Direction { // mark 1
case up, down, left, right
}
struct AStarPuzzle { // mark 2
var heuristics: Int
var boardPathStateList: [[[String]]]
}
class PuzzleSolver { // mark 3
var state: [[String]] = []
let endState = [["1","2","3"], // mark 4
["4","5","6"],
["7","8","0"]]
func availableMoves(state: [[String]]) -> [[[String]]] { // mark 5
var possibleBoardStates: [[[String]]] = []
let tmpState = state
if let i = tmpState.firstIndex(where: { $0.contains("0") }),
let j = tmpState[i].firstIndex(of: "0") {
if i < 2 {
possibleBoardStates += (movePieceInDirection(.down, board: state, piece: (i, j)))
}
if i > 0 {
possibleBoardStates += (movePieceInDirection(.up, board: state, piece: (i, j)))
}
if j < 2 {
possibleBoardStates += (movePieceInDirection(.right, board: state, piece: (i, j)))
}
if j > 0 {
possibleBoardStates += (movePieceInDirection(.left, board: state, piece: (i, j)))
}
}
return possibleBoardStates
}
func movePieceInDirection(_ direction: Direction, board: [[String]], piece: (Int, Int)) -> [[[String]]] { // mark 6
var movements: [[[String]]] = []
switch direction {
case .up:
var boardCopy = board
let tmp = boardCopy[piece.0][piece.1]
boardCopy[piece.0][piece.1] = boardCopy[piece.0 - 1][piece.1]
boardCopy[piece.0 - 1][piece.1] = tmp
movements.append(boardCopy)
case .down:
var boardCopy = board
let tmp = boardCopy[piece.0][piece.1]
boardCopy[piece.0][piece.1] = boardCopy[piece.0 + 1][piece.1]
boardCopy[piece.0 + 1][piece.1] = tmp
movements.append(boardCopy)
case .left:
var boardCopy = board
let tmp = boardCopy[piece.0][piece.1]
boardCopy[piece.0][piece.1] = boardCopy[piece.0][piece.1 - 1]
boardCopy[piece.0][piece.1 - 1] = tmp
movements.append(boardCopy)
case .right:
var boardCopy = board
let tmp = boardCopy[piece.0][piece.1]
boardCopy[piece.0][piece.1] = boardCopy[piece.0][piece.1 + 1]
boardCopy[piece.0][piece.1 + 1] = tmp
movements.append(boardCopy)
}
return movements
}
func misplacedPiecesHeuristic(state: [[String]]) -> Int { // mark 7
var misplaced = 0
var comparator = 1
for line in state {
for number in line {
if number != "\(comparator)" {
misplaced += 1
}
comparator += 1
}
}
return misplaced
}
func aStarSearch(start: [[String]]) -> AStarPuzzle { // mark 8
var explored = [[[String]]]() // mark 9
var pathList = [AStarPuzzle(heuristics: misplacedPiecesHeuristic(state: start), boardPathStateList: [start])] // mark 10
var path: AStarPuzzle = AStarPuzzle(heuristics: 1, boardPathStateList: [])
while true { // mark 11
let currentBestHeuristicIndex = pathList.indices.reduce(0, { pathList[$1].heuristics < pathList[$0].heuristics ? $1 : $0 }) // mark 12
path = pathList.remove(at: currentBestHeuristicIndex) // mark 13
//pathList.removeAll() to greedy solve with more steps but much less space
let finalStateBoardFromBestHeuristic = path.boardPathStateList.last!
if explored.contains(finalStateBoardFromBestHeuristic) { continue } // mark 14
for movement in availableMoves(state: finalStateBoardFromBestHeuristic) { // mark 15
if explored.contains(movement) { continue }
let heuristic = path.heuristics + misplacedPiecesHeuristic(state: movement) + misplacedPiecesHeuristic(state: finalStateBoardFromBestHeuristic) // mark 16
let new = path.boardPathStateList + [movement]
pathList.append(AStarPuzzle(heuristics: heuristic, boardPathStateList: new))// mark 17
}
explored.append(finalStateBoardFromBestHeuristic)
if finalStateBoardFromBestHeuristic == endState { // mark 18
break
}
}
return path
}
}
// mark 19
var board: [[String]] = [["1","5","2"],
["4","8","3"],
["7","0","6"]] // easy board
//var hardBoard: [[String]] = [["3","2","1"],
// ["4","6","5"],
// ["7","0","8"]]
let puzzleSolver = PuzzleSolver()
let puzzleSolved = puzzleSolver.aStarSearch(start: board)
let path = puzzleSolved.boardPathStateList
for index in puzzleSolved.boardPathStateList.indices {
print("State Number \(index + 1)")
path[index].forEach({print($0)})
}
Explaining The A* Algorithm in Swift
Let’s comment on each one of the marks in the code above so we can explain everything that is happening.
- Mark 1 – Just the enum representing each direction that one piece can go.
- Mark 2 – This struct represents the list of board states of that heuristic. This means that all the past board states are stored here and the heuristic Integer value.
- Mark 3 – The PuzzleSolver class is where all the functions and the algorithm itself will be.
- Mark 4- This is the end state of the puzzle, we will compare all the solutions with this.
- Mark 5 – This function calculate all the possible moves for any board state. And the 6. return is a list of those moves.
- Mark 6 – This function just makes the move to return a new board state.
- Mark 7 – The Heuristic part is here. Our heuristic is pretty simple, just calculate how many pieces are out of place. The minimum value for this function is 1 because even zero in the right position is counted wrong, but this doesn’t mess with the final result.
- Mark 8 – Here is the real algorithm function. It receives a board and returns an AStarPuzzle with the heuristic of the solution and all the steps.
- Mark 9 – The array with the explored board states to not repeat in the feature.
- Mark 10 – The first AStarPuzzle with only the start input board state.
- Mark 11 – Now we will repeat all these steps until finding the one it’s equal to the endState declared in the class.
- Mark 12 – A reduced operator does get the lowest heuristic value.
- Mark 13 – Remove to explore the current lowest heuristic value path from the path list.
- Mark 14 – Check if we already explored that board state.
- Mark 15 – We iterate over all the possible next moves of the board, removing the already explored ones. And we store the new ones.
- Mark 16 – Calculate the heuristic value for the path. Ex: If the path has a heuristic with value 8 and it finds a new path with heuristic value 4, the total heuristic of that path would be 12. If the same path with heuristic value 8 finds another next board state with the value 5, we will store it too but it would be 13 in total.
- Mark 17 – Append the new APuzzleStar to the list of the possible paths.
- Mark 18 – Check if this board state is equal to the final state, so we can finish the while loop.
- Mark 19 – Test the algorithm.
After mark 19 you have two boards, one easy to solve and one hard. The hard one can be solved easily by an iPhone because in Playground it doesn’t optimize the space and became too slow.
The Greedy A* Algorithm in Swift
With a simple change, you can remove the comment //pathList.removeAll() and solve it with greedy graph search algorithm. The greedy algorithm will only choose the next best decision. It will find the answer quickly but not necessarily the best one.
When I run the hard state board with the greedy algorithm it took 324 steps to find the solution. When the A* took only 21 steps but with a lot more time and memory consumption.
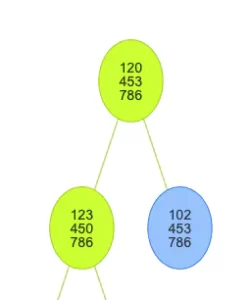
The result of the easy board with A* Algorithm should be:
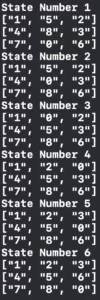
And… that’s it for today!
Algorithms: Continue Studying
The most famous graph algorithms are BFS and DFS, with them you can solve a really big number of algorithmic problems. Check in this article how is the simplest way to use them in Swift.
Trees are a kind of directed graph and you can solve a myriad of problems with them. One of them is how to pruning trees in your code in this article. There we use recursion to check from the leaf to the trunk what are the good branches and which branches should be cut.
Summary – A* Algorithm in Swift
Choosing the A* search algorithm will provide you with the best possible answer to your problem with the memory usage drawback. Choosing the greedy one, you may find the answer with almost zero memory cost but not necessarily the best solution.
What algorithm you will choose depends on your problem constraints. You can play with other algorithms and better visualization on this amazing site of eight puzzle online.
This article couldn’t be done without the help of my dear friend Tales Conrado because it’s his implementation, I just tweaked some variable names and some code cleanup.
That’s all my people, I hope you liked reading this article as much as I enjoyed writing it. If you want to support this blog you can Buy Me a Coffee or leave a comment saying hello. You can also sponsor posts and I’m open to freelance writing! You can reach me on LinkedIn or Twitter and send me an e-mail through the contact page.
Thanks for reading and… That’s all folks.
Credits:






