Hello everyone, Leo here. The topic today is BFS and DFS templates algorithms for problems and what is the minimum code you can have to achieve them in Swift.
Today we’ll explore two very important concepts that are crucial for problem-solving that involves traversing graphs, trees, etc. Those two algorithms are the foundation of knowledge to solve a LOT of graph and tree problems. The importance of knowing those two cannot be underestimated that is why is so important to have them clearly in your head.
So let’s go!
The Problem – BFS and DFS Templates Algorithms
I need to traverse some data structures in breadth or in depth.
Long story short, the difference will be the structure you use to traverse. When using BFS we use a queue to store the next nodes to process. When using DFS the stack is the way to go for processing items.
You can follow up on this article using the Xcode playground file, and I strongly recommend doing that. Let’s suppose a classic tree example.
struct SimpleTree {
var value : Int
var children : [SimpleTree]?
}Just a struct with value and his children. And we can populate the tree with this info:
var simpleNode = SimpleTree(value: 2, children: [SimpleTree(value: 5, children: nil), SimpleTree(value: 6, children: nil)]) var simpleRoot = SimpleTree(value: 1, children: [simpleNode, SimpleTree(value: 4, children: nil), SimpleTree(value: 3, children: [SimpleTree(value: 12, children: nil)])])
Resulting in this structure:
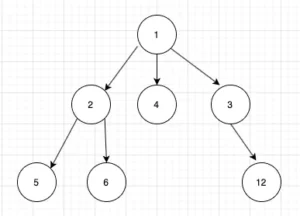
Now that we created the initial structure set up we can start diving into the simplest versions of BFS and DFS in Swift.
The BFS Template – Breadth-First Search
This approach in this case will traverse one level at a time. First, we process the root node, second, we process all the children of the root, third, we process all the children of children of the root node and so goes on.
It’s important to think of BFS as a wider search than an exhaustive search, unlike when you are searching the first thing to match some criteria.
The code follows:
func resolveBFS(_ tree: SimpleTree) -> [Int] {
var result = [Int]()
var queueTree = [tree]
while !queueTree.isEmpty {
let current = queueTree.remove(at: 0) // FIFO - remove the first entry
result.append(current.value) // process node
if let children = current.children { // here you explore all the children, if was a binary tree you should just explore left and right node, for example.
for tree in children {
queueTree.append(tree)
}
}
}
return result
}The implementation above uses the print function as a “processor” of each node, but on your real implementation, you should just do what you are searching for there.
The BFS uses a queue as a backing data structure but curiously we can use swift’s array implementation as a queue ( remember the *remove(at:)* operation in swift is O(N), so be careful)
The result of the code above is:
![]()
You can see, we first visited the root, after that we visited the next level, and so on.
The DFS Template – Depth First Search
In the DFS we can use the same template but instead of using a queue(FIFO), we can use a stack(LIFO). The logic is every time we have to process the next element, we always process the last one inserted, this way going deeper into the data structure.
func resolveDFS(_ tree: SimpleTree) -> [Int] {
var stackResult = [Int]()
var stackTree = [tree]
while !stackTree.isEmpty {
let current = stackTree.popLast() // remove the last one added, O(1)
guard let currentUnwrap = current else {return stackResult}
stackResult.append(currentUnwrap.value) // process node
if let children = currentUnwrap.children {
for tree in children {
stackTree.append(tree)
}
}
}
return stackResult
}And the result is:
![]()
You can observe that in the DFS case we first process the 12 after returning to node 4. This demonstrates that the algorithm is going Deep First and only after it processed all the children of their first child from the root, it would look to the second child and continue going deep until it has exhausted all the children’s possibilities.
It’s amazing what you can get only with these two templates. You should try it yourself!
Wrap-up of BFS and DFS Templates Algorithms
If you want to try the whole template, just copy and paste the code into your playgrounds:
struct SimpleTree {
var value : Int
var children : [SimpleTree]?
}
var simpleNode = SimpleTree(value: 2, children: [SimpleTree(value: 5, children: nil), SimpleTree(value: 6, children: nil)])
var simpleRoot = SimpleTree(value: 1, children: [simpleNode,
SimpleTree(value: 4, children: nil),
SimpleTree(value: 3, children: [SimpleTree(value: 12, children: nil)])])
func resolveBFS(_ tree: SimpleTree) -> [Int] {
var result = [Int]()
var queueTree = [tree]
while !queueTree.isEmpty {
let current = queueTree.remove(at: 0) // FIFO - remove the first entry
result.append(current.value) // process node
if let children = current.children {
for tree in children {
queueTree.append(tree)
}
}
}
return result
}
print(resolveBFS(simpleRoot).debugDescription, "BFS")
func resolveDFS(_ tree: SimpleTree) -> [Int] {
var stackResult = [Int]()
var stackTree = [tree]
while !stackTree.isEmpty {
let current = stackTree.popLast() // remove the last one added, O(1)
guard let currentUnwrap = current else {return stackResult}
stackResult.append(currentUnwrap.value) // process node
if let children = currentUnwrap.children {
for tree in children {
stackTree.append(tree)
}
}
}
return stackResult
}
print(resolveDFS(simpleRoot).debugDescription, "DFS")And we are done!
Algorithms: Continue Studying
Recursion is a powerful tool in your algorithmic toolbox. You can even reverse a linked list using it, did you know that? In that article you will learn how to reverse a linked list using recursion and ace your algorithms interviews in Swift.
Talking about linked lists, it is important to learn another great pattern of using fast and slow pointers in your linked list problems. One of the problems you can solve with that pattern is the odd-even problem in Leetcode.
Summary
Today we studied how to implement the basics of DFS and BFS templates algorithms in Swift. This is just the first step into graphs algorithms and if you have any doubts don’t hesitate to ask me. In the future, I’ll write more articles explaining more deep algorithms like this, so stay tuned for more!
That’s all my people, I hope you liked reading this article as much as I enjoyed writing it. If you want to support this blog you can Buy Me a Coffee or leave a comment saying hello. You can also sponsor posts and I’m open to freelance writing! You can reach me on LinkedIn or Twitter and send me an e-mail through the contact page.
Thanks for the reading and… That’s all folks.
Credits – image






