Hello, Swift enthusiasts and coding aficionados! Today, we’re diving into an exciting journey through the world of dynamic programming, as we tackle a popular problem from LeetCode: the “Climbing Stairs” challenge.
This fun yet challenging problem is a fantastic opportunity to explore the principles of dynamic programming and how it can be elegantly applied in Swift.
But first, let’s talk a bit about dynamic programming. If you’re new to this concept, think of it as a method of solving complex problems by breaking them down into simpler sub-problems. It’s like solving a puzzle – you start with small pieces (sub-problems), solve each one, and then piece them together to solve the bigger picture (the main problem). Dynamic programming is all about optimization and efficiency, especially when you’re dealing with problems that have overlapping sub-problems.
I usually hate dynamic programming questions. Really. I’m never able to just think out of the box the formula to solve the problem, however, the problem today is an exception to that.
So, grab your Swift compiler, and let’s embark on this coding adventure together. We’ll start with understanding the problem in-depth, discuss the dynamic programming approach to solve it, and then dive into the Swift code to make it all happen.
Let’s get coding! But first…
Painting of The Day
Today’s painting is called House with Vine and Staircase by the famous Henri Martin.
Martin, originally from Toulouse and the son of a French cabinet maker and an Italian-descent mother, managed to convince his father to support his artistic aspirations. He embarked on his artistic journey in 1877 at the Toulouse School of the Fine Arts, studying under Jules Garipuy and also learning from Henry-Eugéne Delacroix.
I chose this painting because it depicts a staircase as the problem we will solve today!
The Problem – Climbing Stairs Challenge in Swift
How many distinct ways can you climb a staircase if you can climb either 1 or 2 steps at a time?
The challenge is this: https://leetcode.com/problems/climbing-stairs.
In the case of the “Climbing Stairs” problem, we’ll see how this approach can significantly simplify our code and improve its performance. The question is deceptively simple: How many distinct ways can you climb a staircase if you can climb either 1 or 2 steps at a time? Sounds straightforward, right? But as you delve into it, you’ll realize that it’s a great example to apply dynamic programming.
I KNOW that there exists a mathematical approach to this problem, but we won’t use it this time.
Let’s dive into the solution.
Code Solution – Climbing Stairs Challenge
To solve this I want to start to break the problem into the smallest pieces that we can think of, this is the principle of dynamic programming.
The simplest step is the first one. The first step, the 1, can only be done [1] way. Nice.
Now let’s think about the second step, it can be achieved in two ways, the combination of [1,1] and [2].
Let’s think one more step, and you will start to get to the point. The third step can be done using [ [1,1,1], [2,1], [1,2] ]. With a total of 3 possibilities.
Now visualize the problem until now:
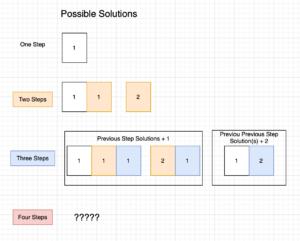
As you can see the Three steps solution is nothing more than, the first-step solutions plus 2 and all the two steps plus one. This way the Four steps solutions would be all of Two Steps solutions plus 2, adding all the three steps solutions plus 1. So the two-step solution had 2 as the answer and the three-step solution had 3 as the answer therefore the four steps solution would be 5.
This works because the problem constrains the possible number of steps that we can have at once, we can only add one or two steps.
At this point you can recognize this as “pseudo-fibonacci” and yes, that would be a math way to solve this. But today we will build a much more straightforward algorithm using dynamic programming. Since we just need to know the previous two answers for the problem to generate the next, we can just solve the first so that all the others can be automatically generated by the algorithm.
Turning all this reasoning into pseudo-code would be:
- Solve the problem for the first and second cases and store their results. If the target is 1 or 2 you can already return the result.
- Since we already solved for 1 and 2 steps, we can subtract 2 from the target since the minimum it could be now is 3.
- For all the next cases we have to store the newest result in a temporary variable.
- Sum the current oldest with the current newest stored values and override the newest store value.
- Override the oldest value with the temporary variable that we created in step one.
- Repeat until we hit our target.
Really simple isn’t it?
Check the Swift solution below:
class Solution {
func climbStairs(_ n: Int) -> Int {
if n == 1 {
return 1
}
if n == 2 {
return 2
}
var result = [1,2]
var target = n - 2
for x in 0..<target {
let temp = result[1]
result[1] = result[0] + result[1]
result[0] = temp
}
return result[1]
}
}Big O Complexity Analysis
As our algorithm doesn’t solve using math, we use a little more space than just creating a recursive function to do that.
The Time Complexity is O(N) where N is the number of steps.
And the Space Complexity is O(1) because for any number of N we will always use the same space in memory because we have used dynamic programming to solve it. Cool, isn’t it?
And that’s it for today!
Solving the Climbing Stairs Problem With Swift
In conclusion, the “Climbing Stairs” problem from LeetCode offers a compelling foray into the realm of dynamic programming, showcasing its power in solving complex problems through the decomposition into simpler sub-problems. This challenge, while appearing simple at first glance, unravels into a fascinating application of dynamic programming principles.
The Swift solution we explored underscores the efficacy of this approach, demonstrating how breaking the problem down into its elemental steps – one and two – allows for a seamless construction of a solution that scales with the problem’s complexity.
Fellow iOS Developers, that’s all. I hope you liked reading this article as much as I enjoyed writing it.
If you want to support this blog you can Buy Me a Coffee or say hello on Twitter. I’m available on LinkedIn or send me an e-mail through the contact page. You can likewise sponsor this blog so I can get my blog free of ad networks.
Thanks for the reading and…
That’s all folks.
Image credit: Featured Painting





