Hello ladies and gentlemen, Leo here. Today we’ll study a tree-like data structure called Trie in Swift. It’s a special type of tree and its main use in the modern world is the core of autocorrect(autocomplete) algorithms.
Will be a great journey into this amazing data structure. At the end of the article, you’ll know exactly what to blame when you want to say Duck and it transforms to Luck.
Trie in Swift – Theory-crafting
First thing first, what is a Trie?
In computer science, a trie, also called digital tree or prefix tree, is a kind of search tree —an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings. […] All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Keys tend to be associated with leaves, though some inner nodes may correspond to keys of interest. Hence, keys are not necessarily associated with every node.
The Trie has a faster lookup than an imperfect hash map, doesn’t has key collision and the main use is to represent string dictionaries. You can see a image representation of a trie below:
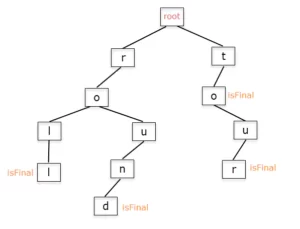
Let’s code!
The problem
Let’s suppose that you have to write an autocomplete algorithm. For example, you enter the prefix “car” and the algorithm must return all the stored complete words that have the “car” prefix.
First, we have to write the TrieNode and the Trie itself structure:
class TrieNode<T: Hashable> { // 1
var value: T? // 2
weak var parentNode: TrieNode?
var children: [T: TrieNode] = [:] // 3
var isTerminating = false // 4
var isLeaf: Bool {
return children.count == 0
}
init(value: T? = nil, parentNode: TrieNode? = nil) {
self.value = value
self.parentNode = parentNode
}
func add(value: T) {
guard children[value] == nil else {
return
}
children[value] = TrieNode(value: value, parentNode: self)
}
}
class Trie { //this is the Trie itself, the root node is always empty
public var count: Int {
return wordCount
}
fileprivate let root: TrieNode<Character>
fileprivate var wordCount: Int
init() { // the initialization of the root empty node
root = TrieNode<Character>()
wordCount = 0
}
}Let’s explain each comment number:
- Note that the Node is generic but the Trie isn’t
- The value of each node (like any other tree) is optional because you need to be able to have an empty root node.
- The related characters.
- This is important because you can have in your Trie a middle node(not leaf) that is also a word termination.
With these two classes, we can now start to write our two algorithms: the insert function and search words in subTrie.
The Swift’s Trie Insert Function
Copy paste the insert function below:
extension Trie {
func insert(word: String) {
guard !word.isEmpty else {
return
}
var currentNode = root
for character in word.lowercased() { // 1
if let childNode = currentNode.children[character] {
currentNode = childNode
} else {
currentNode.add(value: character)
currentNode = currentNode.children[character]!
}
}
guard !currentNode.isTerminating else { // 2
return
}
wordCount += 1
currentNode.isTerminating = true
}
}- In The first part, we are traversing all the children nodes until the end of the word and if you find the character you just add it just became the new current node if not, we just add it to the current node and it became the current node.
- This is to prevent counting two times the same word.
And now… it’s the time we’re all waiting: the function words in sub-Trie.
extension Trie {
func findWordsWithPrefix(prefix: String) -> [String] {
var words = [String]()
let prefixLowerCased = prefix.lowercased()
if let lastNode = findLastNodeOf(word: prefixLowerCased) { //1
if lastNode.isTerminating { // 1.1
words.append(prefixLowerCased)
}
for childNode in lastNode.children.values { //2
let childWords = getSubtrieWords(rootNode: childNode, partialWord: prefixLowerCased)
words += childWords
}
}
return words // 3
}
private func findLastNodeOf(word: String) -> TrieNode<Character>? { // this just check is the prefix exist in the Trie
var currentNode = root
for character in word.lowercased() {
guard let childNode = currentNode.children[character] else { // traverse the Trie with each of prefix character
return nil
}
currentNode = childNode
}
return currentNode
}
}We’ll start explaining the findWordsWithPrefix:
- This traverse the Trie trying to find the last node that matches the prefix and after that(1.1) checks if the prefix itself is a word( isTerminating)
- Now we begin to traverse the last node children to get all the words that have the prefix.
- Return the found words.
And finally, the wordsInSubtrie function and it’s the heart of all this algorithm so we have to give it special attention:
extension Trie {
fileprivate func getSubtrieWords(rootNode: TrieNode<Character>, partialWord: String) -> [String] {
var subtrieWords = [String]()
var previousLetters = partialWord
if let value = rootNode.value { // 1
previousLetters.append(value)
}
if rootNode.isTerminating { //2
subtrieWords.append(previousLetters)
}
for childNode in rootNode.children.values { //3
let childWords = getSubtrieWords(rootNode: childNode, partialWord: previousLetters)
subtrieWords += childWords
}
return subtrieWords
}
}
- This check and unwrap if the node has a value ( always should have but it’s safe to do the “if let” check here).
- Now we have to check if the currentNode is a terminating node, which means it’s a word!
- And again we traverse the child nodes searching for all the terminating words recursively.
And Voilà we finished the basic structure of the autocorrect/autocomplete algorithm!
I recommend copying and pasting all the code to the playgrounds and you can play/study around it. It’s an amazing algorithm and you can upgrade it to a way more complex implementation, like giving weights to each node so when returning to the user you can also suggest the most used word or the most “correct” word.
To test it write:
var trie = Trie() trie.insert(word: "car") trie.insert(word: "care") trie.insert(word: "carrot") trie.insert(word: "carb") trie.insert(word: "carburized") trie.insert(word: "cardboard") trie.insert(word: "carrousel") trie.insert(word: "carries") print(trie.findWordsWithPrefix(prefix: "carb")) print(trie.findWordsWithPrefix(prefix: "carr")) print(trie.findWordsWithPrefix(prefix: "car")) print(trie.findWordsWithPrefix(prefix: "cat"))
And the result should be:

Algorithms: Continue Studying
You don’t need to write all the algorithms yourself. Sometimes you can leverage language features to build better code, and you can discovery that you can use the Swift tuple structure to make complex sort operations.
A famous tree algorithm is to merge two binary trees. You can achieve that in a few lines of code, check the article to learn how to do that!
Summary
I hope you had a great time discovering/remembering this algorithm as I had, and when the autocorrect just turns your life into hell we can certainly say: BLAME YOU TRIE! Now you know how to make a Trie in Swift and that’s amazing, right?
That’s all my people, I hope you liked reading this article as much as I enjoyed writing it. If you want to support this blog you can Buy Me a Coffee or leave a comment saying hello. You can also sponsor posts and I’m open to freelance writing! You can reach me on LinkedIn or Twitter and send me an e-mail through the contact page.
Thanks for the reading and… That’s all folks.
Credits: image





