Odd Even Linked List Problem in Swift

Hallo vrienden, Leo Hier. The topic today is how to solve the Odd Even Linked List problem in Swift.

Today we will explore a linked list problem. Linked lists are a very curious data structure because you can have a lot of variants of them. For example, you can have a Doubly linked or a singly linked, which means if the nodes of the list have a link to the next node only or they have a link to the next node and a link to the previous node.

A lot of computer science problems involve linked lists, a very common example is pagination. When we deal with pagination a very common implementation is using a doubly linked list, this way you can go forward and backward with ease.

No more talking, let’s code. But first…

Painting of The Day

The painting is a 1913 art piece called Morning in the Village after Snowstorm by the painter Kazimir Severinovich Malevich. He was a Russian avant-garde artist and art theorist, whose pioneering work and writing had a profound influence on the development of non-objective, or abstract art, in the 20th century.

I chose this painting because it says a lot about connecting things. It’s amazing how the painter can connect geometric forms, in this case, he has already assimilated the cubism movement and made us think of abstractions of reality instead of the reality itself.

The problem – Odd Even Linked List Problem in Swift

Given the head of a singly linked list, group all the nodes with odd indices together followed by the nodes with even indices, and return the reordered list.

You can check the details in the leetcode problem.

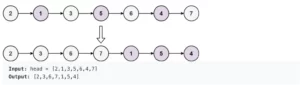
So imagine that we have now a linked list and we rearrange the nodes of it. The way we will rearrange is that every node with the odd index will be grouped on the left side of the linked list, and the nodes with an even index will be grouped in the right side of the linked list.

The image below is the example we are trying to achieve.

Implementation – Solving the Linked List Problem

The first thing that pops into my mind is: let’s create two pointers, one for the odd linked list and one for the even linked list. After I have those two pointers, I’ll traverse the list updating the pointers and in the end, I connect the final node of the odd list with the head node of the even list.

The implementation will use two pointers, as many of the linked list solutions uses. The knowledge to manipulate pointers is very important when writing algorithms using linked lists.

And that’s exactly what we are going to do now:

func oddEvenList(_ head: ListNode?) -> ListNode? {
    var oddList: ListNode? = head // Mark 1
    var evenList = head?.next // Mark 2
    let evenHead = evenList // Mark 3
    
    while (evenList != nil && evenList?.next != nil) { // Mark 4
        oddList?.next = evenList?.next // Mark 5
        oddList = oddList?.next // Mark 5
        
        evenList?.next = oddList?.next // Mark 6
        evenList = evenList?.next // Mark 6
    }
    
    oddList?.next = evenHead // Mark 7
    
    return head
}

Explaining the Algorithm Solution

Check the detailed explanation below:

Mark 1 – we create the odd list first element.
Mark 2 – we get the next element of the odd list, which can only be an even to be the start of the even list.
Mark 3 – we save the head of the even list so we can reference that at the end of the algorithm.
Mark 4 – Now we start to traverse the linked list. We will traverse until the point that the even list is not nil, because if it’s nil we just will add it in the end anyway and the next even node list is also not nil because if it doesn’t worth to change the pointers because we will add it at the end of the algorithm anyway.
Mark 5 – Now we will start to update our odd list pointers. The next odd list node should be the next of the current even list. And after that, we update the odd list pointer itself to be that node. We do this to continue traversing the linked list. If we don’t update the oddList pointer will always point to the same node.
Mark 6 – This is exactly the same logic that we did in Mark 5 but now for the even list. The next of the new oddList should be the next of the current evenList and the evenList itself becomes updated with it next.
Mark 7 – As a final step we connect the last node of the oddList to the head node of the evenList, remember we were updating it on each traverse cycle.

And that’s it!

Continue Studying Algorithms

Permutations is a good way to study strings and it is something that is good to be sharp to do out of the box in interviews. Check this article to solve the permutations problem called “no repeats please”.

Functional programming can be a great tool while you are solving algorithms. Although in many cases the faster way is just to use traditional loops, a functional approach can be very useful for the readability and extensibility of your codebase. Thinking in check the article “solving the shopping cart problem” using functional programming.

Summary – Odd Even Linked List problem in Swift

Today we solved a very nice problem that uses two pointers to reconnect all the linked list nodes in an arbitrary order.

That’s all my people, I hope you liked reading this article as much as I enjoyed writing it. If you want to support this blog you can Buy Me a Coffee or leave a comment saying hello. You can also sponsor posts and I’m open to freelance writing! You can reach me on LinkedIn or Twitter and send me an e-mail through the contact page.